Performant Clustering of Geo Coordinates w/ Custom Distance Functions

Recently I worked on a project triangulating geo-coordinates of signals based on registrations in a radio network. Part of the approach involved clustering observations into distinct geographic regions. The clustering algorithms used weren’t anything special (nearest-neighbor, k-means), however measuring the distance between points in geo-coordinates is not as simple as measuring the distance between points in cartesian coordinates.

Instead of the euclidean distance supported by most clustering algorithms, the ideal metric is Haversine Distance which measures the shortest path between two points traveling along the surface of a sphere.

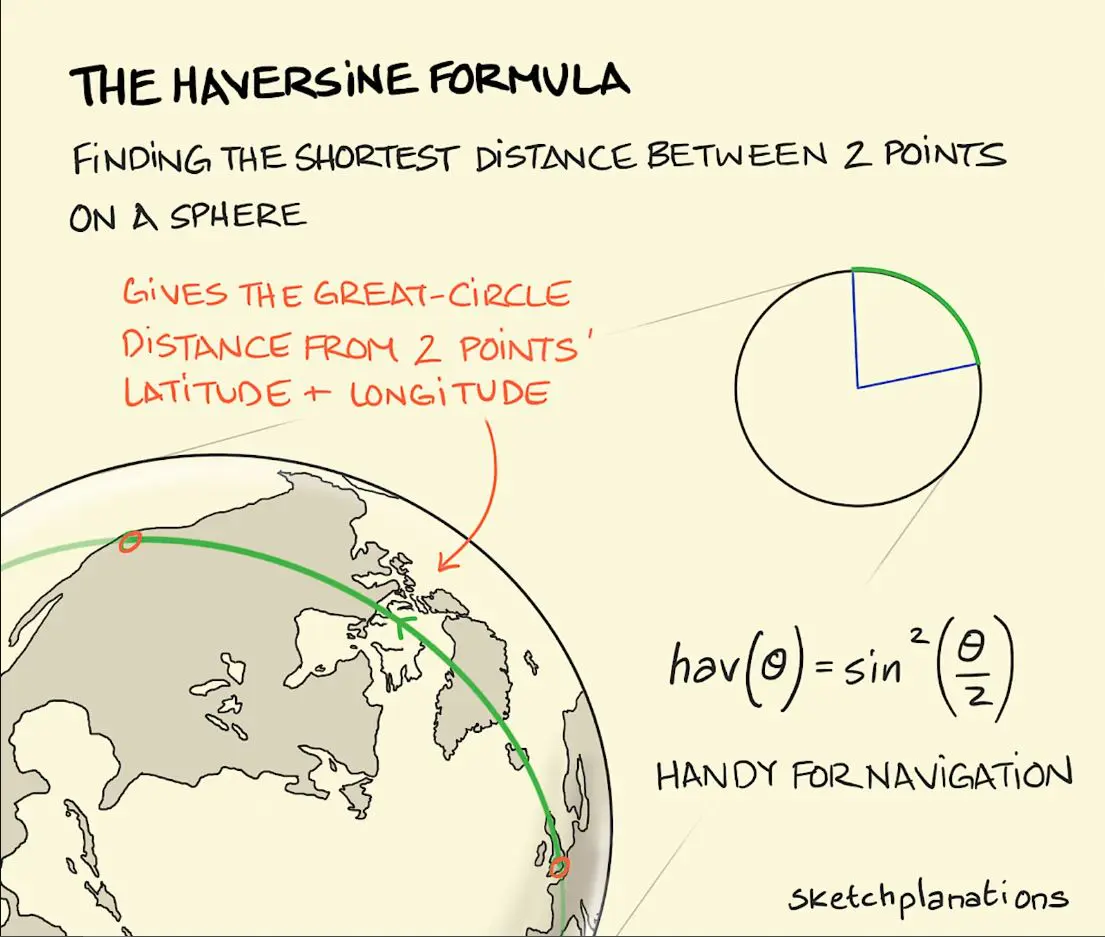
Here is simple numpy implementation:

def haversine_np(
    lat_long_deg_1: npt.NDArray,
    lat_long_deg_2: npt.NDArray,
    radius: float = RADIUS_EARTH_KM,
) -> npt.NDArray:
    """
    Calculate the great circle distance between two points on a sphere
    ie: Shortest distance between two points on the surface of a sphere
    """
    lat_1, lon_1, lat_2, lon_2 = map(
        np.deg2rad,
        [
            lat_long_deg_1[:, 0],
            lat_long_deg_1[:, 1],
            lat_long_deg_2[:, 0],
            lat_long_deg_2[:, 1],
        ],
    )
    d = (
        np.sin((lat_2 - lat_1) / 2) ** 2
        + np.cos(lat_1) * np.cos(lat_2) * np.sin((lon_2 - lon_1) / 2) ** 2
    )
    arc_len = 2 * radius * np.arcsin(np.sqrt(d))
    return arc_len

NOTE: this post is framed around an example of haversine distance, but this technique applies to many different scenarios. Maybe you need to measure the levenshtein edit distance between strings or a compatibility score between potential wedding guests :)

I was shocked to discover that most clustering tool kits (scikit-learn) do NOT support custom distance metrics. Those that do (NLTK) are extremely slow, because they execute a provided distance function for every pair of points individually. This is ok for clustering a handful of data points…. but will NOT scale to millions of samples. Instead I wrote a pseudo vectorized implementation like so:

Nearest-Neighbor

For my problem, I needed relatively even spacing between clusters. For this a nearest-neighbor algorithm was a better choice. While not completely vectorized, this approach scales more linearly than exponentially.

def haversine_cluster(
    points_lat_long_deg: npt.NDArray,
    centroids_lat_long_deg: npt.NDArray,
    trace: bool = False,
) -> npt.NDArray:
    """Cluster points to the closest centroid based on haversine dist

    Args:
        points_lat_long_deg (npt.NDArray): the data points to cluster, shape (n, 2)
        centroids_lat_long_deg (npt.NDArray): the cluster centroids, shape (k, 2)
        trace (bool, optional): If True, display progress bar. Defaults to True.

    Returns:
        (npt.NDArray): labels (cluster indices) for each data point
    """
    # Cluster the data points to the nearest "cluster" based on haversine dist
    n = points_lat_long_deg.shape[0]
    k = centroids_lat_long_deg.shape[0]
    # Assign centroids based on minimum haversine distance
    diff = np.zeros((n, k))
    for i in tqdm(range(k), disable=not trace):
        diff[:, i] = haversine_np(
            points_lat_long_deg, centroids_lat_long_deg[np.newaxis, i, :]
        )
    labels = diff.argmin(axis=1)  # n,
    return labels

# Pre-define grid of clusters  
# TODO: this could be further improved by initializing equidistant centroids (http://extremelearning.com.au/evenly-distributing-points-on-a-sphere/)
# For now, just prune unpopulated clusters afterwards
n_div_lat = 250
n_div_long = 500
cluster_div_lat = np.linspace(np.min(data[:,0]), np.max(data[:,0]),  n_div_lat)
cluster_div_long = np.linspace(np.min(data[:,1]), np.max(data[:,1]),  n_div_long)
centroids = np.zeros((cluster_div_lat.shape[0]*cluster_div_long.shape[0], 2))
for i, lat in enumerate(cluster_div_lat):
    for j, long in enumerate(cluster_div_long):
        centroids[i * n_div_long + j] = [lat, long]

# Then cluster the data points to the nearest "cluster" based on haversine dist
labels = haversine_cluster(
    # use only a subset of data points... since this is expensive
    points_lat_long_deg=data, 
    centroids_lat_long_deg=centroids,
    trace=True
)

# Remove any clusters that have no data points... 
# this reduces the final number of clusters while keeping an even spacing
populated_centroid_idxs = np.array(sorted(np.unique(labels)))
centroids = centroids[populated_centroid_idxs, :]

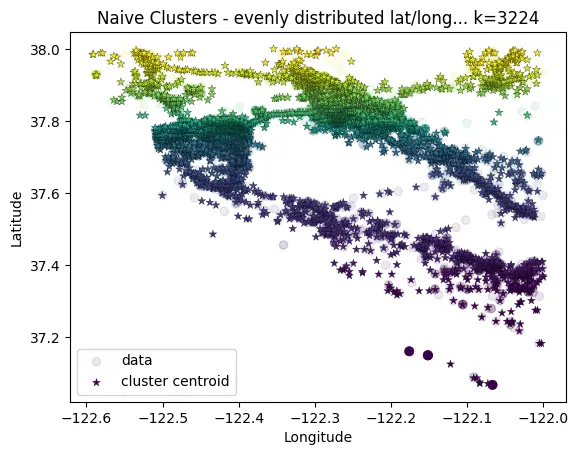
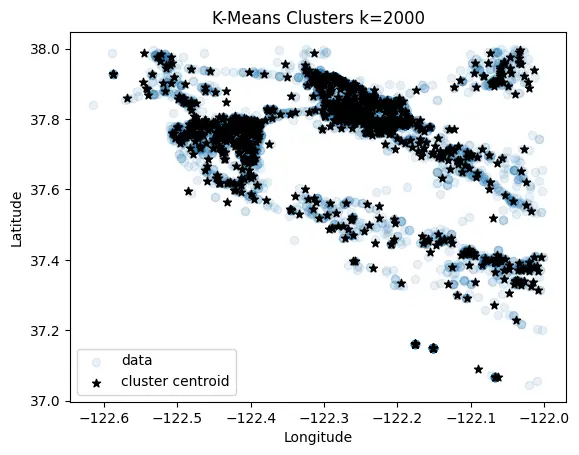
K-Means

A k-means implementation just for grins :)

def k_means(data, k:int=50, num_iter:int=50, seed:int=42, trace: bool=False):
    np.random.seed(seed)

    n, d = data.shape
    data_lla = np.stack([data[:,0], data[:,1], np.zeros((n))])  # 3, n
    
    # Initialize centroids as random selection of data points
    centroids = data[np.random.choice(n, k, replace=False)] # k, d 
    diff = np.zeros((n,k))

    for _ in tqdm(range(num_iter), disable=not trace):
        # Assign centroids based on minimum haversine distance
        for i in range(k):
            diff[:, i] = haversine_np(data, centroids[np.newaxis, i,:])
        labels = diff.argmin(axis=1) # n,

        # Update the centroids to be the projected centroid of the members of each cluster
        for i in range(k):
            member_idxs = np.argwhere(labels==i).squeeze()
            members = data_lla[:, member_idxs] # 3, x
            if members.shape[-1] == 0:
                # empty cluster... don't update
                continue
            centroid = calculate_centroid_geo(lat_long_alt=members.swapaxes(0,1)) if members.ndim > 1 else members
            centroids[i] = centroid[:2]
        break
    return centroids

For more details see associated repository https://github.com/dcyoung/ml-triangulation